1. Probability Values Range from 0 to 1

The probability of an event lies within the range of 0 to 1:

• If an event cannot occur, P(A) = 0.
• If an event is guaranteed to occur, P(A) = 1.

For instance, rolling a 7 on a standard six-sided die is impossible, so its probability is 0. Conversely, flipping a coin will always yield either heads or tails, making that probability 1.

2. How to Calculate Probability

When outcomes in a sample space are equally likely, the probability of an event is calculated by dividing the number of favorable outcomes by the total number of possible outcomes:

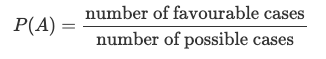
For example, rolling a 3 on a six-sided die has a probability of:

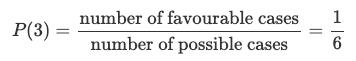
This is because there is one favorable outcome (the face showing 3) and six total possible outcomes (the six faces of the die).

3. Understanding the Complement of an Event

The probability of the complement (the opposite) of an event can be expressed as:

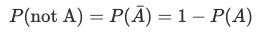
For instance, the probability of not rolling a 3 is:

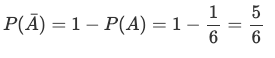
4. Union of Two Events

The probability of the union of two events is the probability of at least one occurring:

P(A or B) = P(A) + P(B) - P(A and B)

For example, consider the probability of a fire occurring in two houses within a year:

• In house A: P(A) = 0.6
• In house B: P(B) = 0.45
• In at least one of the two houses: P(A and B) = 0.8

Graphically represented, this can be calculated as:

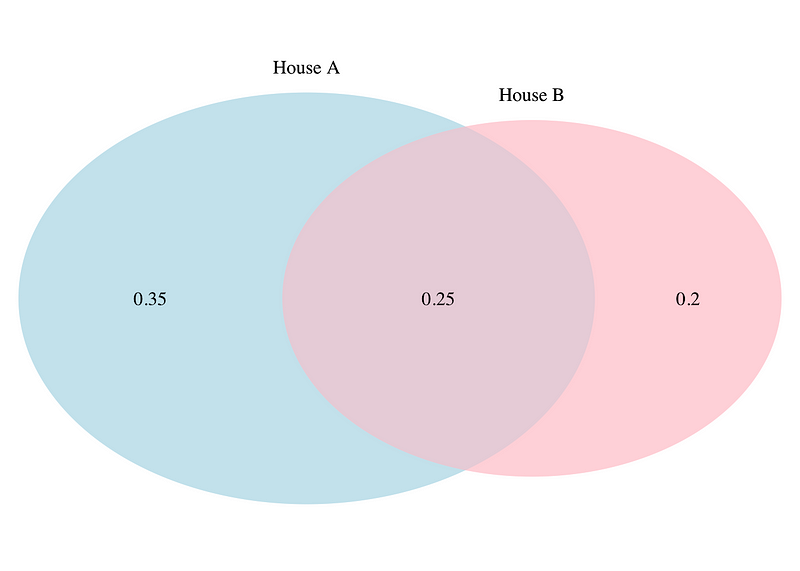
5. Intersection of Two Events

If two events are independent, the probability that both occur together (intersection) is given by:

P(A and B) = P(A) * P(B)

For instance, if two coins are flipped, the probability of both showing tails is:

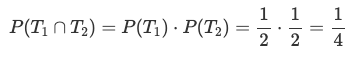
6. Independence of Events

Two events are independent if the occurrence of one does not affect the other. This can be checked using the formula above. If it holds true, the events are independent; otherwise, they are dependent.

7. Conditional Probability

The conditional probability of event A given event B occurs is expressed as:

P(A|B) = P(A and B) / P(B)

Note that P(A|B) is not generally equal to P(B|A). This can lead to the derivation of Bayes’ theorem, which is crucial for many statistical applications.

The first video titled "5 Concepts in Statistics You Should Know | Data Science Interview" provides a concise overview of essential statistical concepts that can aid in data science interviews.

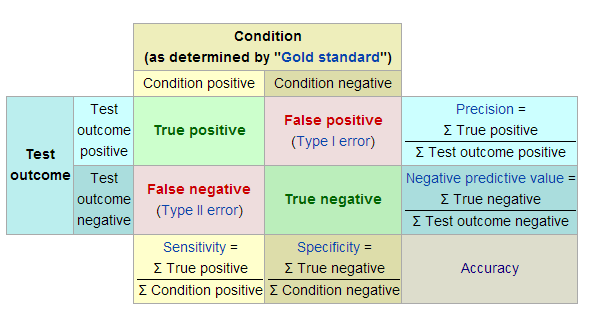
8. Accuracy Measures

To evaluate the performance of probabilistic models, various accuracy measures are employed, including:

• False negatives
• False positives
• Sensitivity
• Specificity
• Positive predictive value
• Negative predictive value

Here’s a visual representation of these measures within a diagnostic context:

9. Counting Techniques

To utilize the formulas effectively, one must understand how to count possible outcomes. The main counting techniques include:

• Multiplication
• Permutations
• Combinations

For example, in a restaurant offering 2 starters, 3 main courses, and 2 desserts, the total number of meal combinations can be calculated as:

2 * 3 * 2 = 12

The second video titled "How to ACTUALLY Learn the Math for Data Science" provides practical insights into mastering the mathematical foundations necessary for data science.

In conclusion, mastering these fundamental probability concepts and formulas is vital for any aspiring data scientist. If you have questions or suggestions related to this topic, please feel free to leave a comment for further discussion.