Exploring the Marvel of Quaternions in Navigation Systems
Written on
Introduction to Quaternions
The guidance systems have successfully functioned as intended. On July 24, 1969, the Apollo 11 Command Module, carrying Neil Armstrong, Michael Collins, and Edwin Aldrin, made a safe return to Earth, being hoisted aboard the USS Hornet after its iconic splashdown (Source: Wikipedia). In my previous article, we examined the technologies vital for modern aircraft and spacecraft navigation, which primarily involve sensors that capture a craft's instantaneous angular velocity. This time, we will delve into the theoretical underpinnings that affirm why quaternions are the optimal mathematical tool for converting sensed angular velocity into an accurate orientation estimate for spacecraft or aircraft.
Guidance is Internal!
In this section, we will explore the mathematical coincidences that underscore the power of quaternions as a non-commutative skew field, which, despite their complexity, provide a natural extension of Euler's famous identity.
Mathematical Foundations of Quaternions
The remarkable state of quaternions is rooted in several profound mathematical coincidences. They serve as an intricate yet effective method for processing orientation data in three-dimensional space. Unlike the traditional imaginary unit (i) from complex analysis, quaternions allow us to utilize any member of a unit sphere within a three-dimensional complex framework. This unique algebraic structure makes quaternions indispensable in modern navigation systems for aircraft and spacecraft.
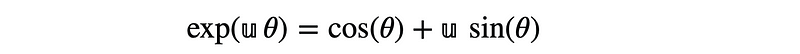
The Sylvester Matrix Representation illustrates how quaternions uniquely extend the complex number system.
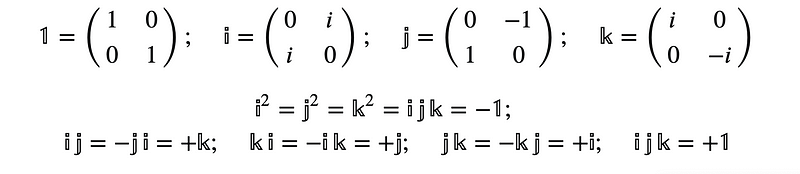
Trisecting Angles and Higher Dimensions
We explore why real numbers can only extend to fields of dimensions 1, 2, 4, and 8, and how this relates to quaternions.
The Algebraic Structures of Quaternions
Quaternions provide the foundation for stable and natural representations of rotations. Their properties enable quicker calculations with greater numerical stability compared to traditional methods.
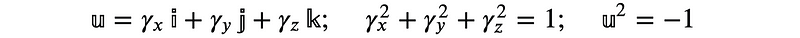
Logarithmic Calculations and Quaternion Units
Exponentials of quaternion units serve as rotation operators akin to Euler's identity in complex numbers. This relationship bridges the gap between Lie Algebra and Lie Group, revealing a profound algebraic coincidence that enhances quaternion utility.
Practical Applications of Quaternions
In practical terms, the Sagnac sensor plays a crucial role in relaying readings across three axes back to the flight computer. These readings are represented as a pure quaternion, capturing the craft's orientation throughout the sampling interval.
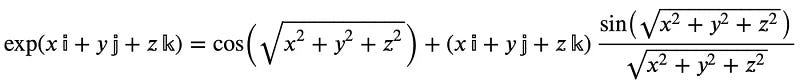
The quaternion's Pythagorean norm effectively represents the rotation angle during the sampling period. This characteristic underpins their use in navigation systems.
Quaternion Representations in Software
Using the Sylvester Unit for quaternion calculations enables efficient updates to the aircraft's orientation based on sensor data. While the quaternion is theoretically unit magnitude, practical considerations necessitate periodic normalization to mitigate roundoff errors.
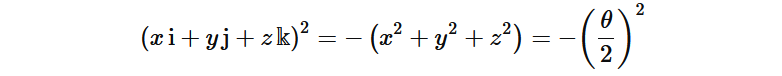
Conclusion and Reflection
In closing, it is essential to recognize the extraordinary mathematical coincidences that establish quaternions as a powerful tool in navigation. Their unique structures not only facilitate efficient calculations but also enhance the reliability of orientation tracking in both aerospace applications and computer graphics.
A Tribute to the Pioneers of Space Exploration
This exploration of quaternions is dedicated to the legacy of the Apollo missions and the remarkable individuals who contributed to humanity's journey into space.

Through this journey, we celebrate the intersection of mathematics, technology, and human ambition, honoring those who have paved the way for future explorations.