Forces and Friction on the Spider Wall

The term "spider wall" might be misleading, as spiders don’t actually scale walls in this manner (even Spider-Man requires only one wall). For our analysis, we will consider a simplified stick-figure ninja with both feet pressed against the wall. Below is a diagram representing the forces at play.

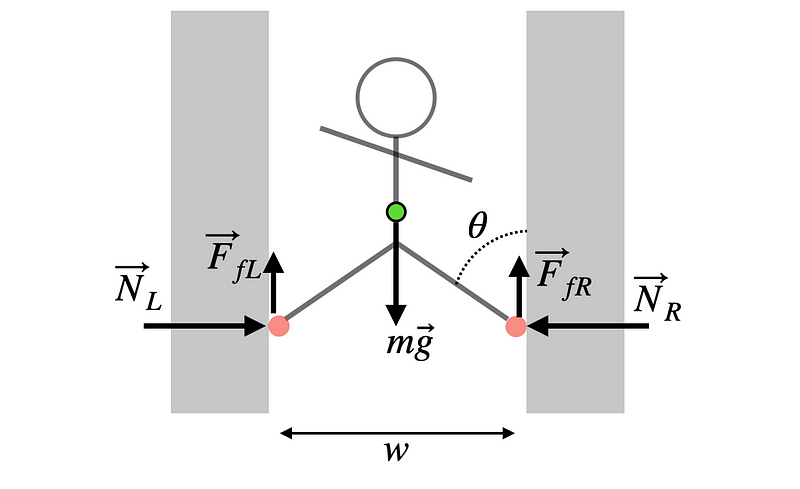
To begin, we need to make certain assumptions. Let's presume the left and right sides of our ninja are symmetrical, meaning the frictional and normal forces exerted on either side are equal.

Next, we must explore how much force is needed to remain on the wall without falling. Remember, ninjas aren't meant to plummet into the water below. By applying Newton’s second law, we find that the vertical forces (in the y-direction) must sum to zero, leading us to the following equation.

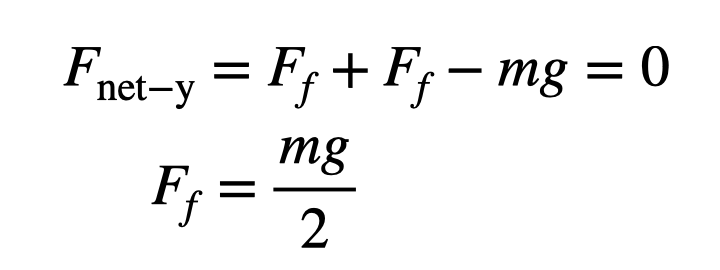
A common model for static friction indicates that the maximum frictional force is directly proportional to the normal force.

In this formula, µ_s represents the coefficient of static friction, which is determined by the interaction between the two surfaces (for example, rubber shoes on plexiglass). Analyzing the horizontal forces doesn’t provide much insight. Essentially, we observe:

Thus, we confirm that N = N, which we already anticipated. However, with knowledge of the friction coefficient, we can calculate the minimum normal force necessary to achieve the maximum frictional value.

Introducing a value for mass (m) and µ_s would yield the normal force but would not specify the force the ninja must exert against the wall. Both the frictional force and normal force act on the foot, meaning the ninja must apply an equal and opposite force according to Newton’s third law. Therefore, we need to ascertain both the frictional and normal forces.

Let’s assume that the combined frictional and normal forces align with the leg at an angle θ. This gives us the following relationship.

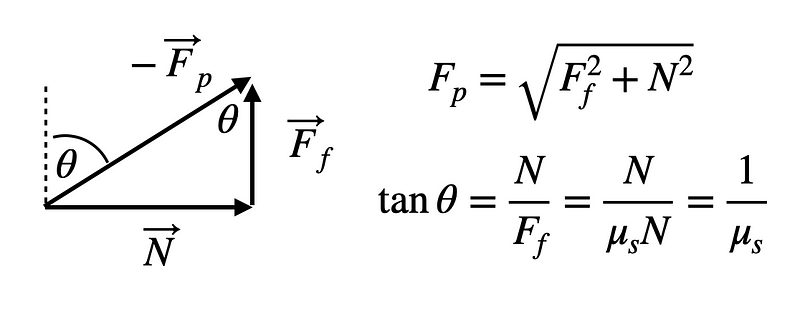
Notice that -F_p represents the force exerted against the wall. This is our primary focus. For now, we can express both N and F_f.

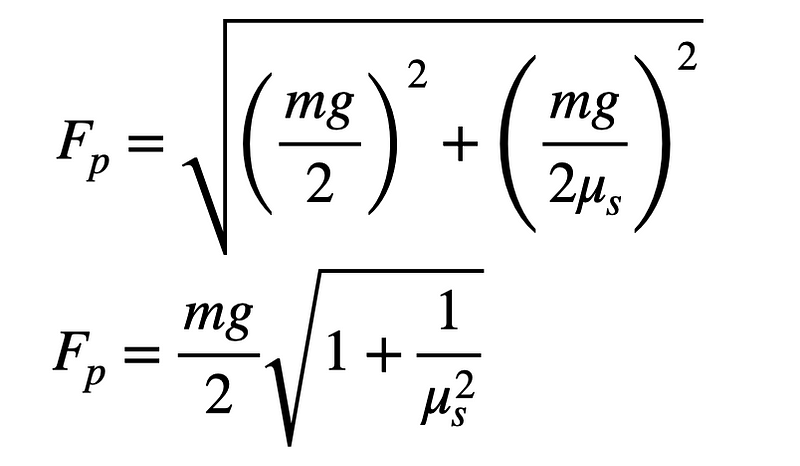
Ultimately, we’ve derived a useful equation. For fun, here's a graph illustrating the force each ninja leg must exert to avoid falling into the water. The vertical axis shows the push force divided by the weight.

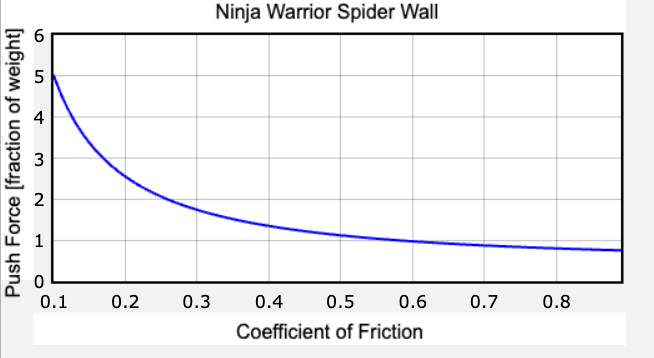
From the graph, it's evident that with very low coefficients of friction (below 0.2), the force required exceeds the ninja's weight per leg significantly. Even with a coefficient around 0.5, a Ninja Warrior would need to exert a force equal to double their weight. It's certainly a tough task to be a ninja!

Now, let's address the question: does cleaning your shoes matter? At low coefficients of friction, even a minor increase can lead to a significant impact. Conversely, if the surface is already relatively sticky, small adjustments won't have much effect. The coefficient for rubber on cardboard ranges from 0.5 to 0.8. Notably, increasing the coefficient from 0.5 to 0.6 results in minimal change in force required. Therefore, wiping your shoes may not be necessary unless they are covered in chalk.

Regarding the angle θ, we can estimate the minimum static friction coefficient required. If we assume that the angle between the legs and the wall is 45 degrees, the coefficient of friction would need to be 1 (1/tan(45)). In reality, the legs will likely need to be positioned at an angle greater than 45 degrees, as the coefficient typically falls below 1.