Understanding Segment Lengths in Triangles Using Stewart's Theorem
Written on
Chapter 1: Introduction to Segment Length Calculation
In certain scenarios, calculating the length of a segment within a triangle can be challenging, especially when angle measures are unknown or difficult to ascertain. In 1746, Scottish mathematician Matthew Stewart introduced a theorem that addresses this issue directly: Stewart's Theorem establishes a connection between the lengths of a triangle's sides and the length of a cevian.
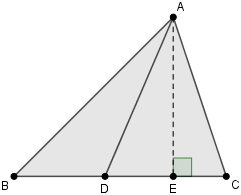
Consider the triangle ABC depicted below.

Let point E be located on line BC such that AE is the altitude of triangle ABC. We denote D as a point on side BC, making AD an arbitrary cevian. Our goal is to express the length of AD in relation to the sides of triangle ABC.
D can occupy two possible positions: between B and E, or between E and C. If triangle ABC is obtuse, E may even fall outside the segment BC. We encourage readers to explore proofs for these variations, as they closely mirror the case we will examine here, which is illustrated in the figure above.
Section 1.1: The Pythagorean Approach
According to the Pythagorean Theorem (Theorem 1.4), we can derive three key equations related to the triangle:
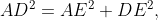
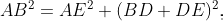
Prepare for an extensive algebraic process. Note the following relationships:

and

By substituting these equations into the equation below, we can derive:
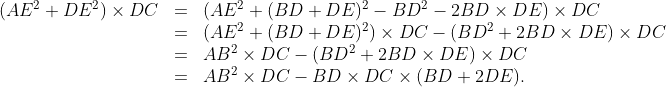
Upon inspection, we observe that all variables in the final equation pertain to the sides of triangle ABC, except for AD². Thus, we have successfully established a relationship between AD and the triangle's sides, which is articulated in Theorem 1.5 below.
Theorem 1.5
For triangle ABC with point D on side BC, the following holds:

Endnote
For those encountering Stewart's Theorem for the first time, it may appear quite complex, and indeed it can be. This complexity arises from the omission of angles in the calculations involving cevians. In future discussions, we will integrate angles when exploring the sine and cosine rules.
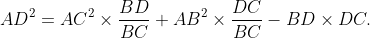
Here, we delve into how to utilize the centroid of a triangle to determine segment lengths, providing visual and conceptual clarity to the process.
This video demonstrates how to use the area of a given triangle to find the length of an unknown line segment, enhancing your understanding of geometric relationships.