Challenging Yet Engaging Australian Calculus Exam Question
Written on
Chapter 1: Introduction to the Exam Question
In the 2023 Mathematical Methods Exam 2, a particularly tough question was posed to Year 12 students in Victoria, Australia. The problem presented was to analyze the function defined as f(x) = n^x - x^n and determine the real number n for which this function achieves a local minimum along the x-axis. This question was likely the most difficult on the exam, with estimates suggesting that fewer than 10% of students managed to solve it.
Students taking the exam were equipped with graphing calculators, specifically those that include a Computer Algebra System (CAS). These advanced calculators offer capabilities such as graphing functions, solving equations, computing derivatives, and executing custom programs.
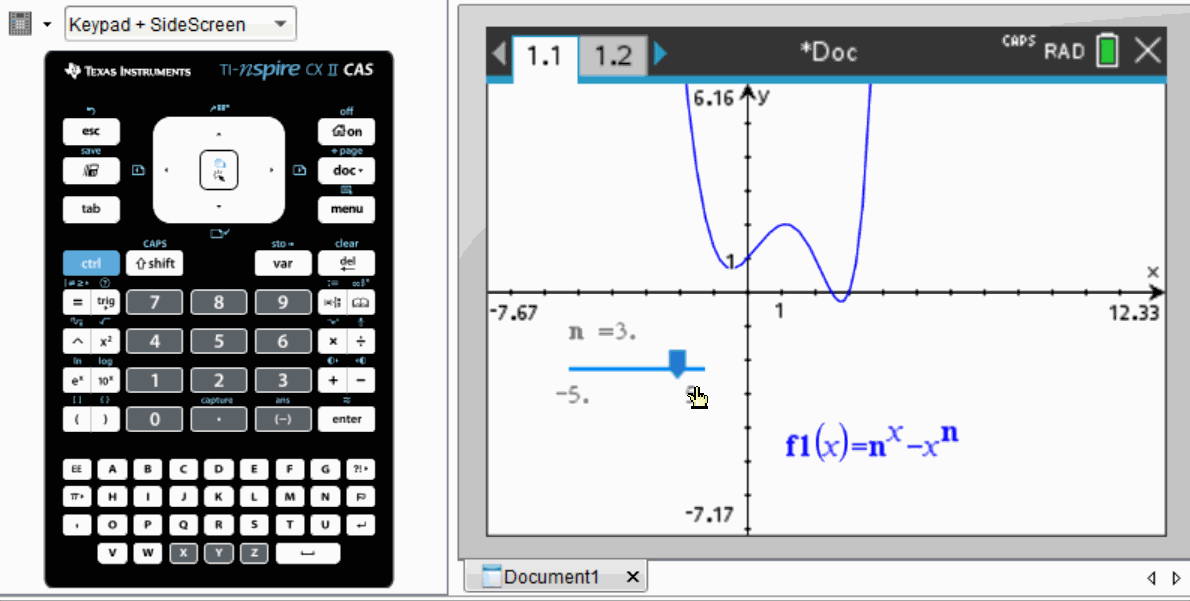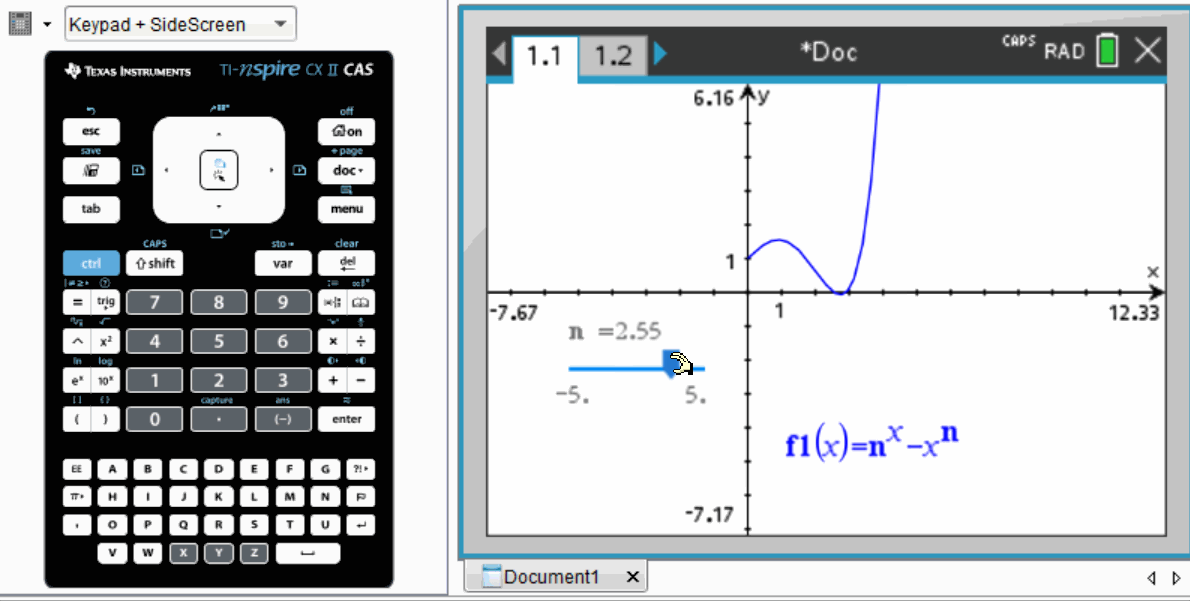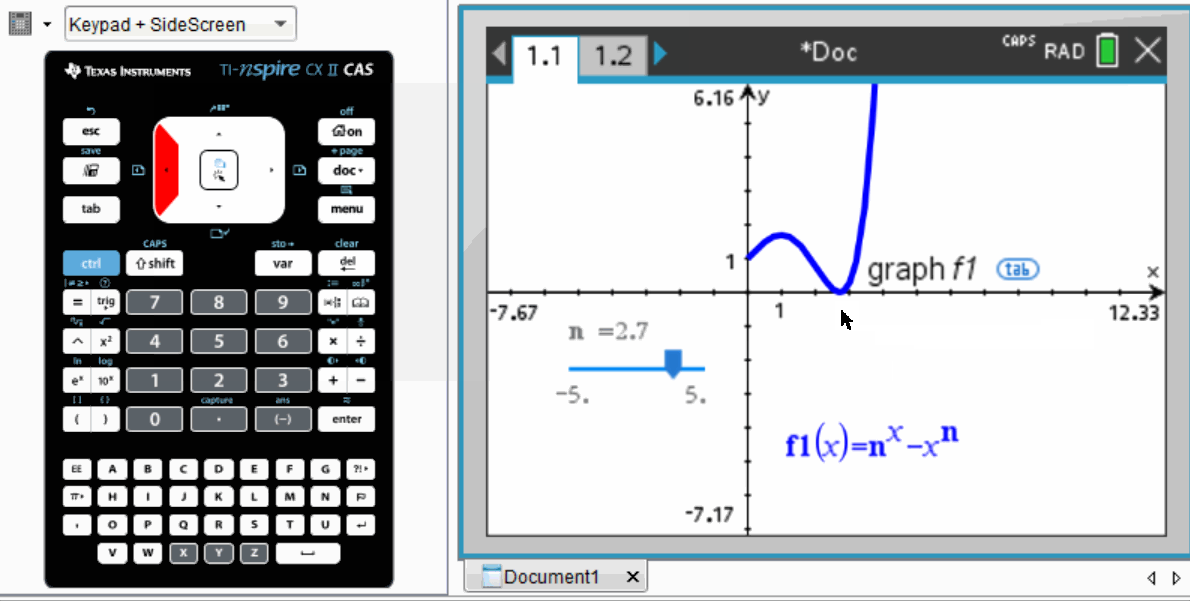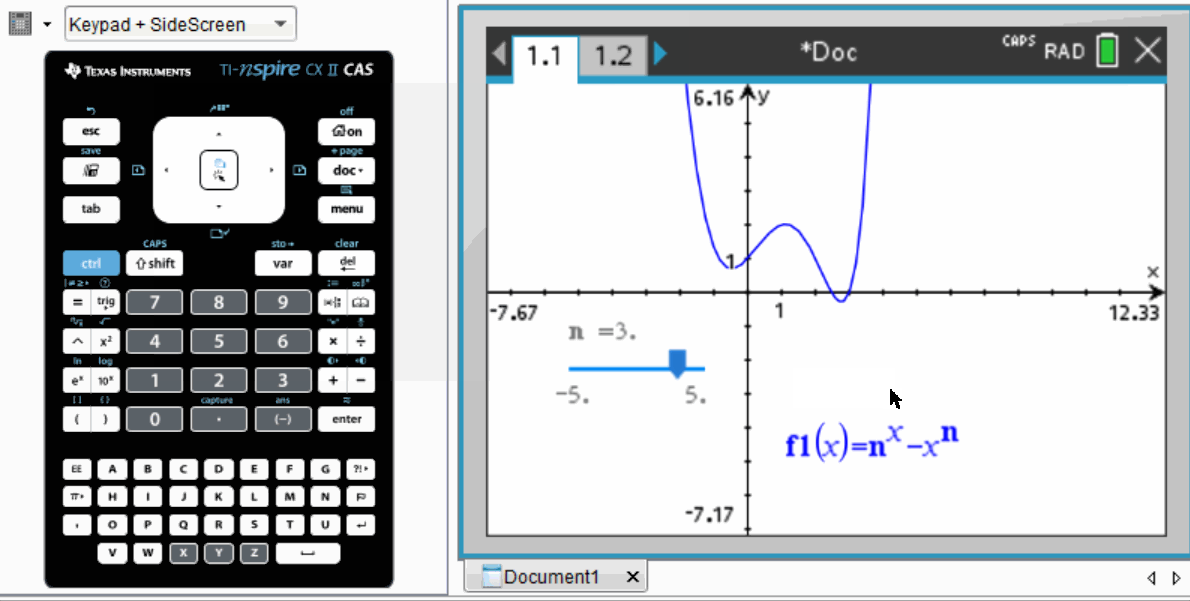
To begin solving this problem, a sensible approach is to graph the function and observe the effects of varying n.

As illustrated, the local minimum approaches the x-axis when n nears 3.
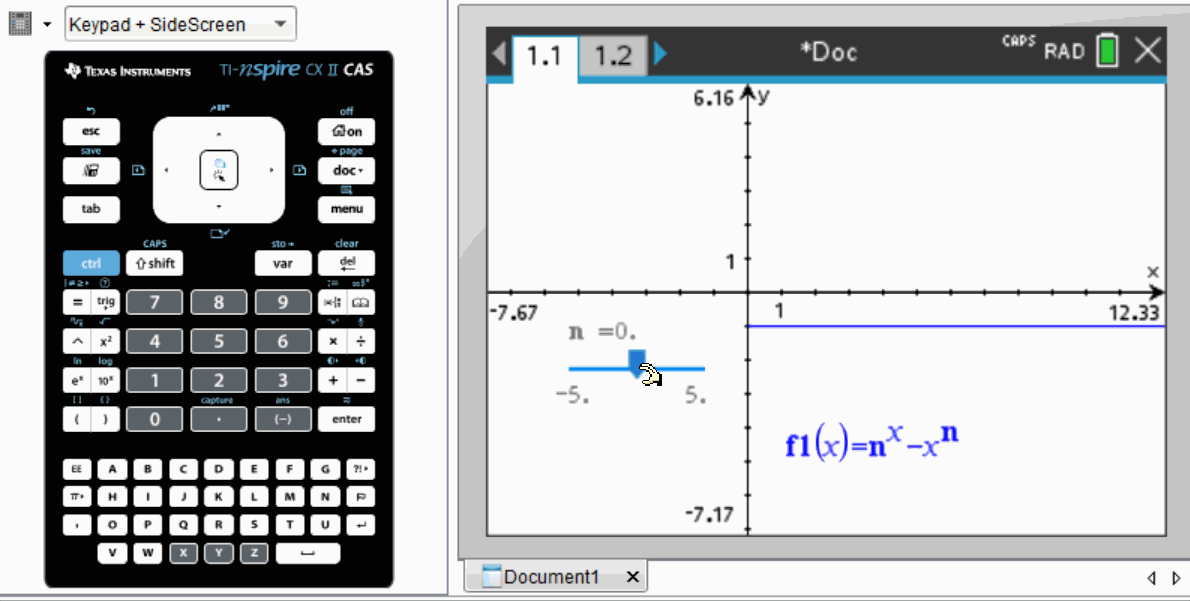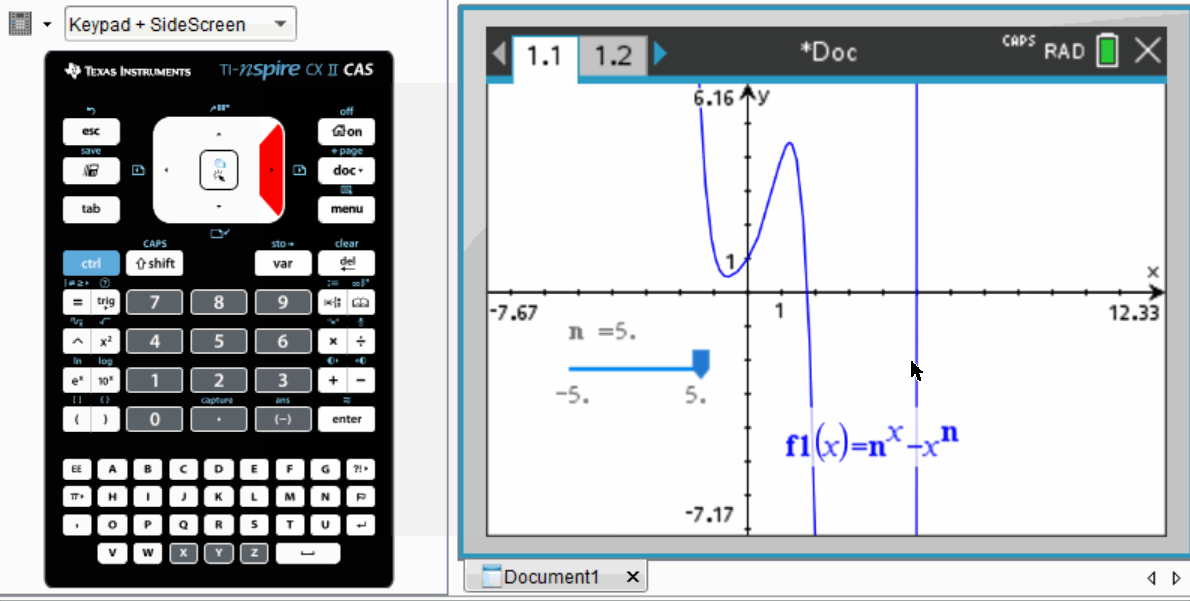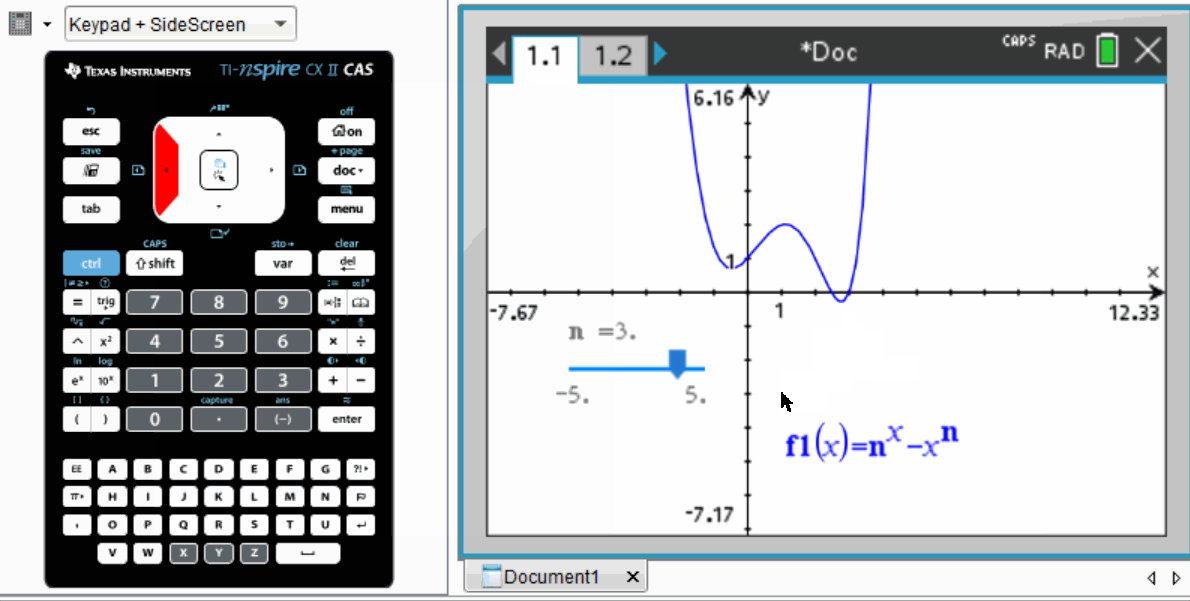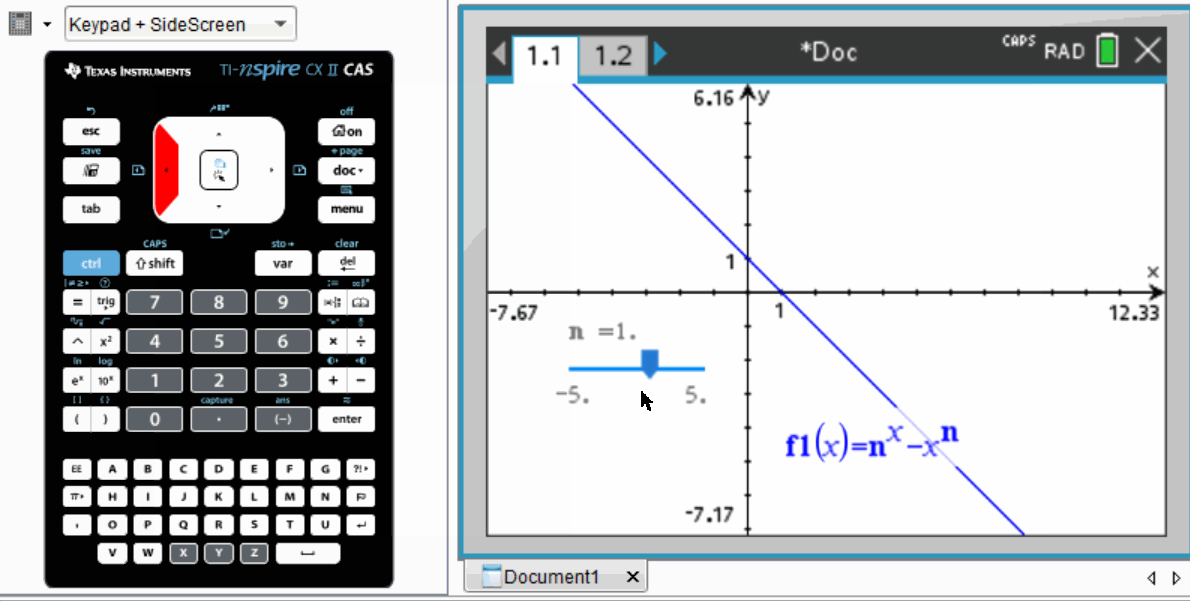
Utilizing the TI-nspire CAS, students can define the function in terms of n and employ a “slider” feature to change n's value. Similar functionality is often found in platforms like Desmos or Geogebra.
By adjusting the slider with precision, it becomes evident that the value of n required is slightly below 3, likely around 2.7.
To achieve an exact result, students must apply calculus principles. They can leverage their calculators to compute the derivative of the function:
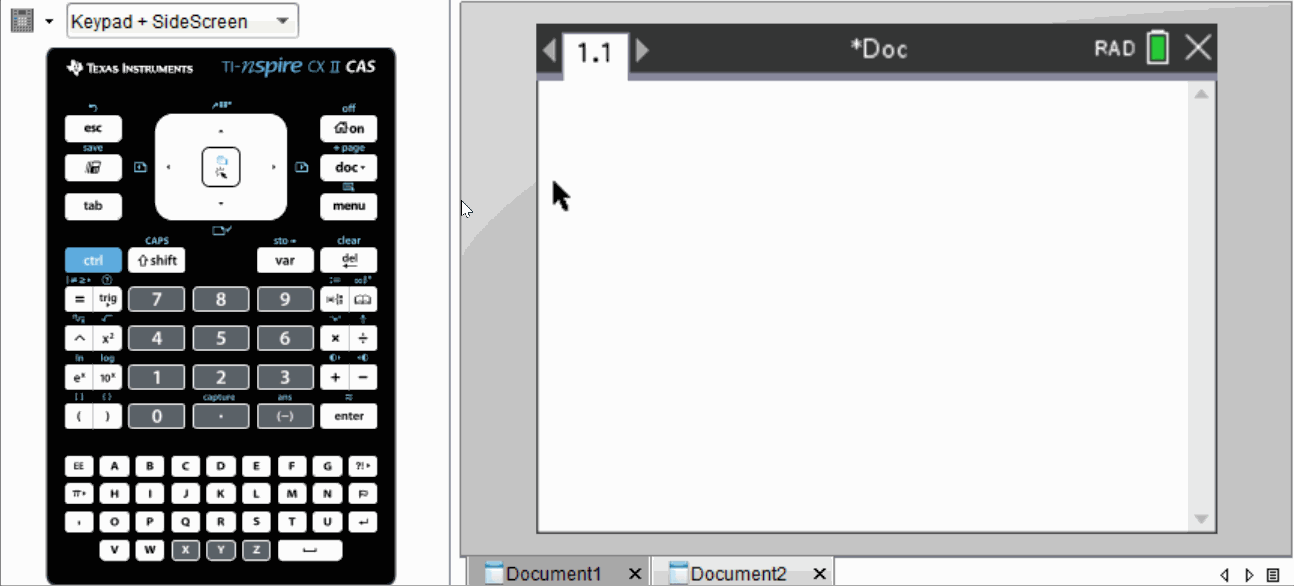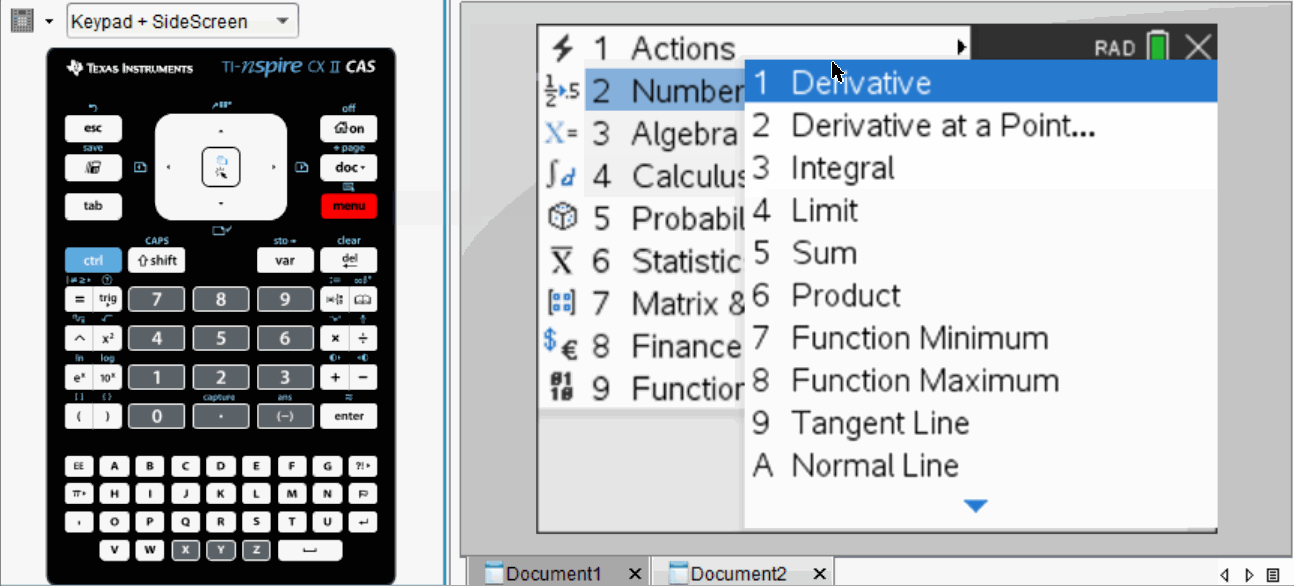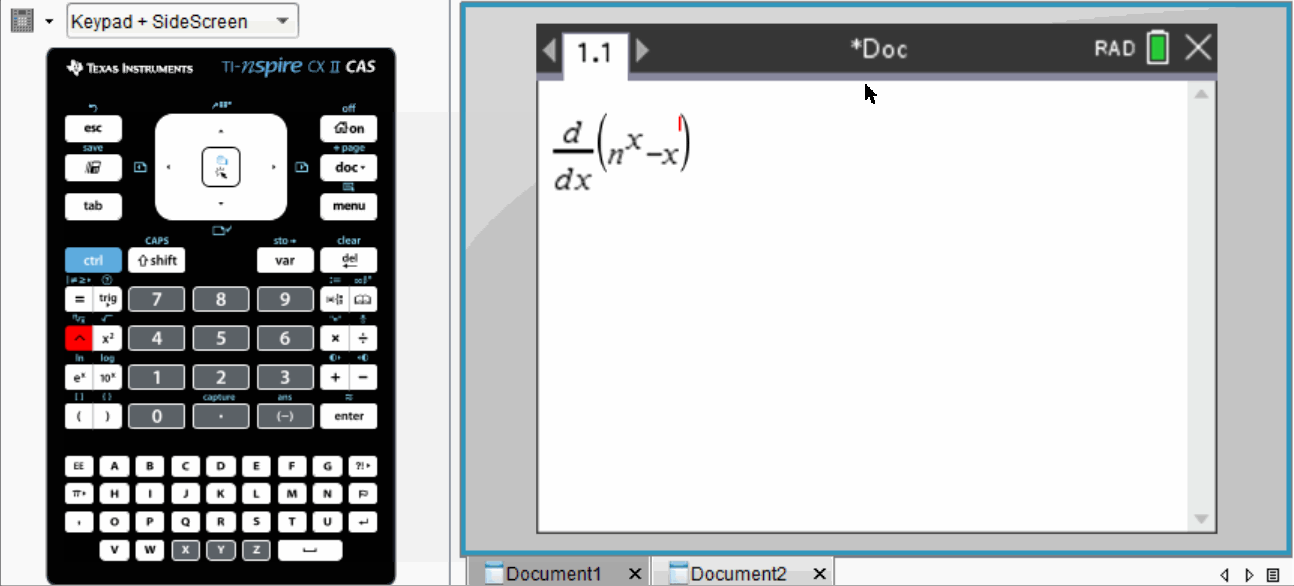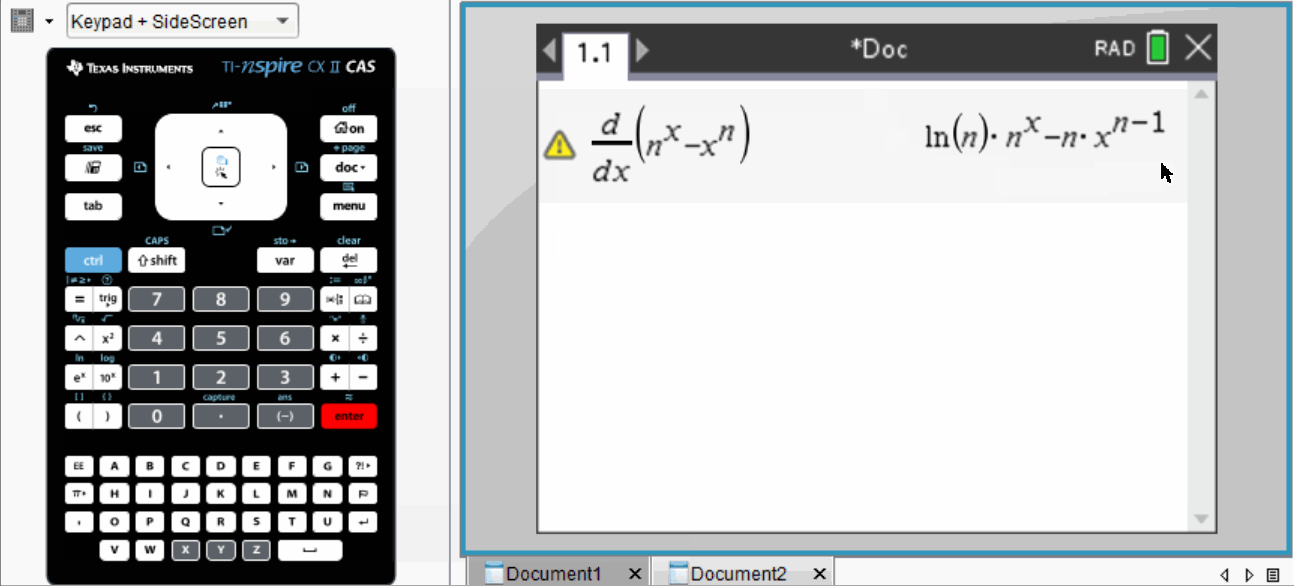
When calculating the derivative manually, it’s necessary to rewrite the exponential term with base e. Then, applying the chain rule, which states that for e^(g(x)), the derivative is g’(x) × e^(g(x)), is essential. The x^n term follows a more straightforward polynomial derivative.
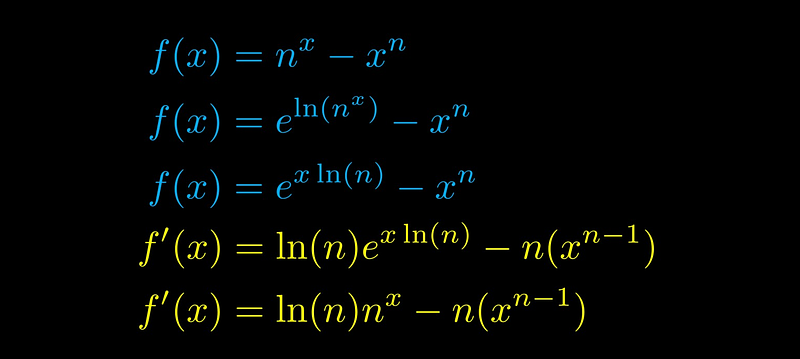
To find a local minimum on the x-axis, we need the derivative to equal zero at the same x value where the function itself also equals zero. This leads us to a pair of significant equations:
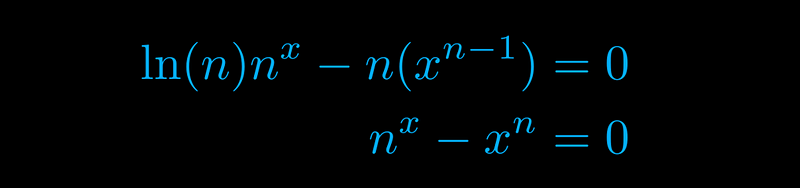
Although the equations are complex, recognizing that f(x) = n^x - x^n will always intercept the x-axis at x = n simplifies our task.
When we examine the graph behavior for various n values, we find that there are at most two positive x-intercepts—one of which is at x = n. As n approaches approximately 2.7, these two intercepts converge into a single repeated root, indicating the presence of a local minimum on the x-axis. Thus, the local minimum must occur when x = n.
Substituting x = n into the initial equation allows us to factor out an n^n term, ultimately leading to the precise solution:
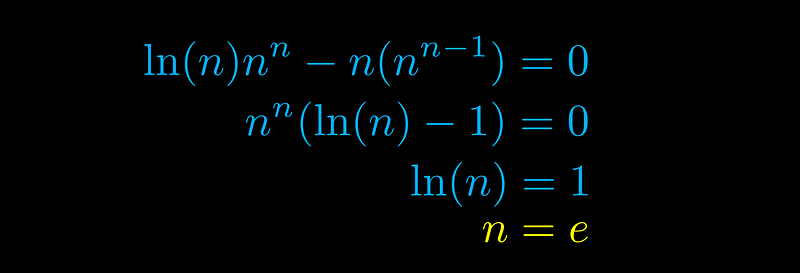
And there it is! 🎉
Did you anticipate that outcome? 🤔