Chapter 1: Introduction to the Gauss Algorithm

Linear equation systems are prevalent in both science and engineering disciplines. There's a common saying in computational physics: ultimately, all problems can be reduced to solving linear equations. In this article, we will explore the essential method for solving such equations by hand—the Gauss Algorithm. Manually solving these systems can be quite labor-intensive, which is why we will leverage Python to handle the calculations for us.

Daily Dose of Scientific Python

Explore common and unique challenges resolved using libraries like Numpy, Sympy, SciPy, and matplotlib.

Chapter 1.1: From Equations to Matrices

Consider the system of equations:

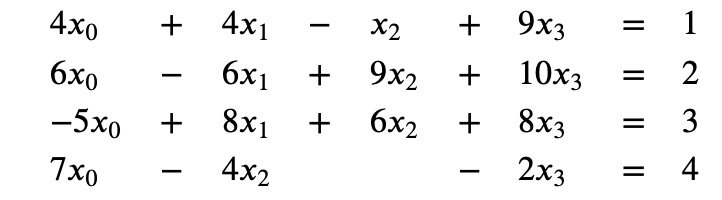
Utilizing the rules of matrix multiplication, this can be expressed in matrix notation as:

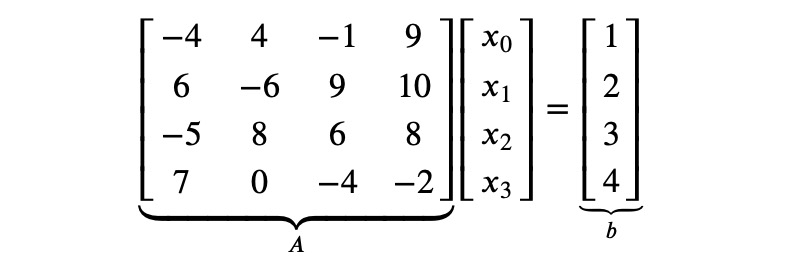
By applying the Gauss Algorithm, we will manipulate both the matrix A and the vector b to arrive at the solution vector x.

Chapter 1.2: Understanding the Algorithm through Examples

To effectively illustrate how the algorithm functions, we will proceed with a practical example. Utilizing Sympy, we can avoid the hassle of manually writing down extensive calculations. Begin by launching a Jupyter notebook and defining the matrix A:

The Gauss Algorithm consists of two phases: forward and backward elimination. Initially, we will focus solely on matrix A, disregarding the right-hand-side vector b.

In the forward elimination phase, we will traverse the diagonal and adjust the matrix so that all diagonal elements become 1, while ensuring that all elements below the diagonal are set to zero. Starting with the top-left element (row 0, column 0), which is -4, we can achieve this by dividing the entire row by -4:

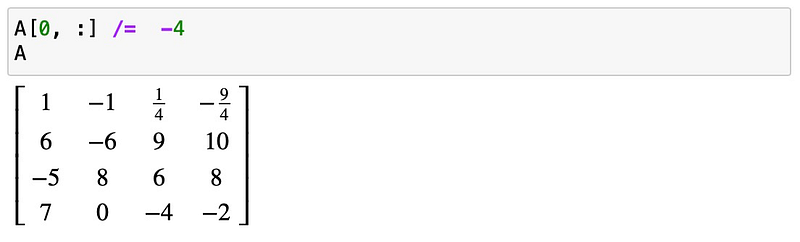
Next, to eliminate the elements below the diagonal, we subtract appropriate multiples of row 0 from the subsequent rows:

This marks our first forward step. Moving to the next diagonal element located in row 1, column 1, which is 0, we encounter a challenge. We cannot divide by zero! In this case, we need to swap the current row with a lower row that has a non-zero element in the same column. Here, we can exchange with row 2, which contains a 3:

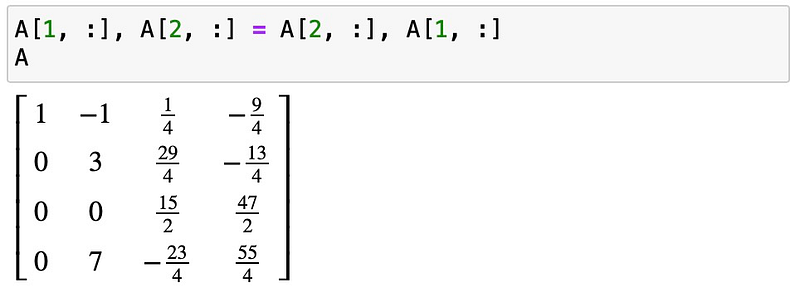
Now we can continue as before. Divide row 1 by 3 to make the diagonal entry 1:

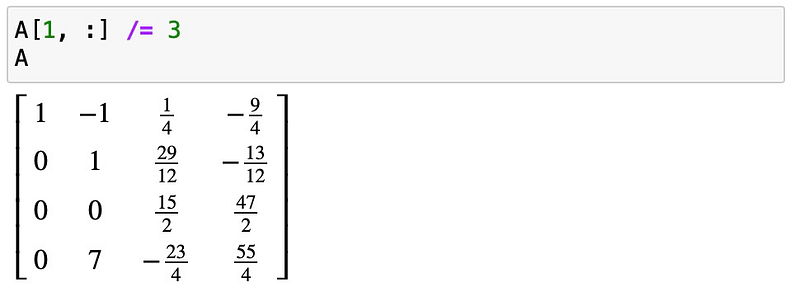
Proceeding row by row, we subtract a suitable multiple of row 1 to eliminate the corresponding elements:

This completes the second forward step. The remaining forward steps are straightforward:

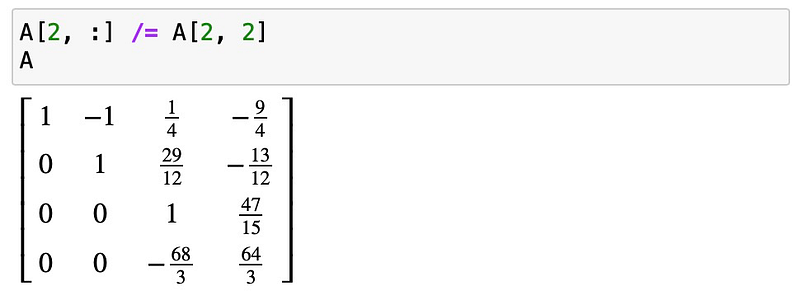
Now that we have an upper triangular matrix with 1s along the diagonal, we move to the backward elimination phase. The objective here is to remove the entries above the diagonal.

Starting with the lower right element in row 3, column 3, we subtract appropriate multiples of the last row to eliminate the entry above it:

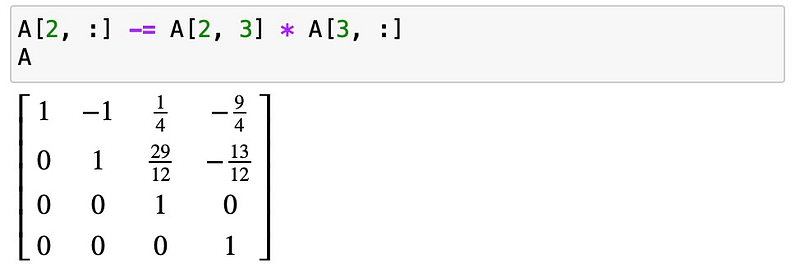
We apply this process for each row until we transform the original matrix into an identity matrix. Why is this significant? It allows us to solve the equations effectively. While manipulating matrix A, we must also adjust the right-hand side vector b accordingly.

Chapter 2: Solving Equation Systems

At the conclusion of this article, you will find a Python implementation that details every step of the Gauss Algorithm for a given problem. We will utilize this for the equation system introduced earlier. Define both the matrix and the right-hand side:

Both will be passed as arguments to the GaussAlgorithm class defined at the end of the article. Execute the algorithm by calling doit():

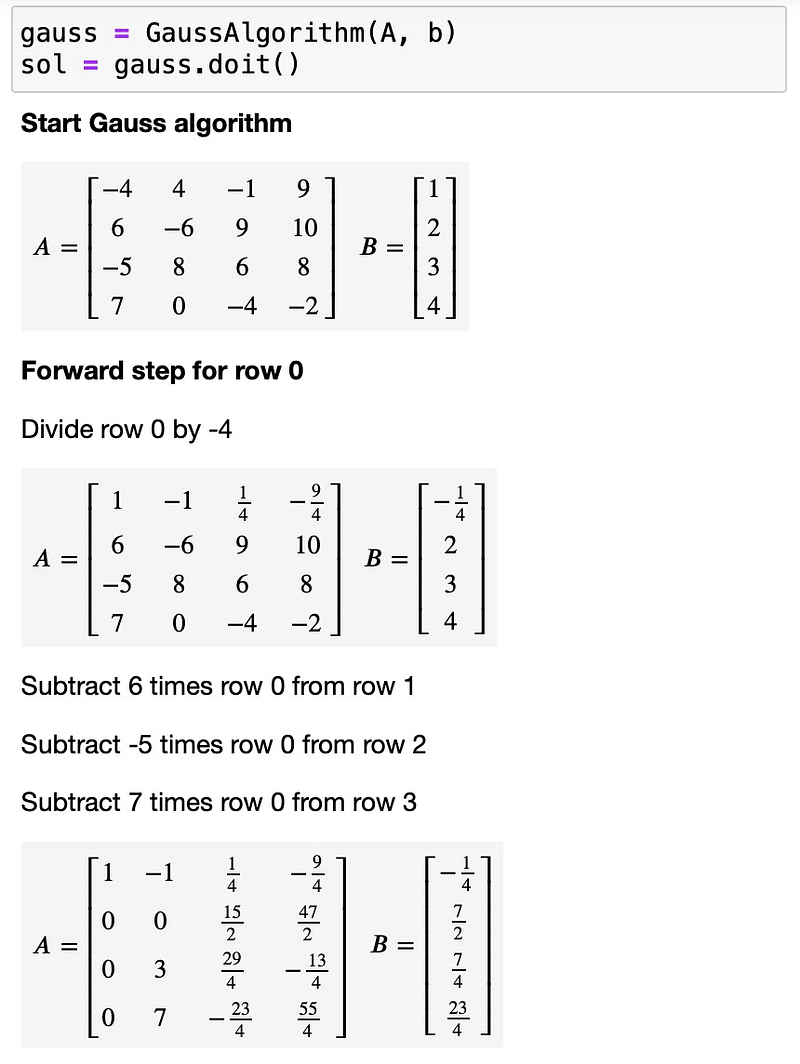
The final step of the Gauss Algorithm reveals the solution to the equation system, illustrated below:

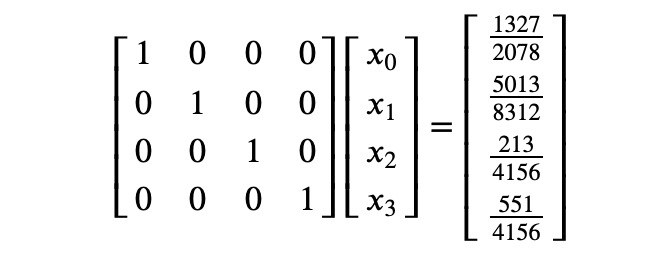
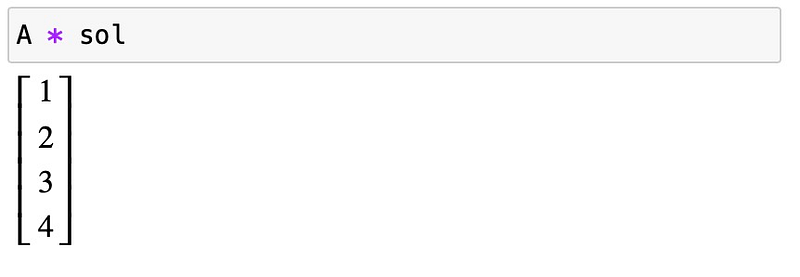
Performing matrix multiplication on the left-hand side should yield the original right-hand side:

Although Sympy can provide the solution instantly:

It's crucial to understand the manual process, as it helps identify potential errors in calculations.

Chapter 2.1: Step-by-Step Implementation in Python

Finally, here is the Python code that implements the step-by-step algorithm discussed above.

Coding the Gauss Elimination Algorithm in Python (ChEn 263 - Supplement to Lecture 11, Fixed!)

Gaussian Elimination In Python | Numerical Methods