The Role of Topology

Topology is fundamentally about understanding how objects can be transformed. For instance, consider how to classify 1-dimensional loops within a 2-dimensional space based on their ability to be deformed. We will denote our space as X.

To illustrate, let’s take X as a sphere.

Starting with any loop on the sphere's surface, we can manipulate it to a single point. If we can achieve this deformation, we say the loop is “equivalent to 0.” Thus, all such loops can be considered as part of a collection that is equivalent to 0. We can notate this as H¹(X, ℝ)=0. Importantly, the initial loop need not be a smooth circle; it can take on a myriad of forms, as long as it remains a closed loop.

Now let’s consider a more complex space, a torus.

In this case, if we begin with a loop that doesn’t traverse the entire torus, it can similarly be deformed down to a point. Conversely, a loop that wraps around the torus can also be reshaped into a simpler form.

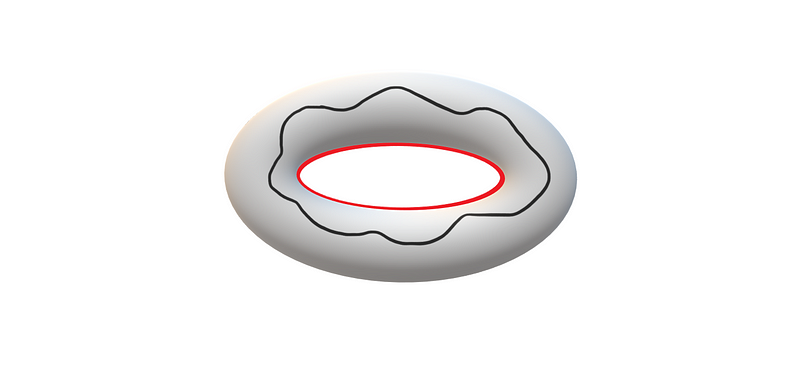
Ultimately, we find that only specific loops generate non-zero elements in this scenario. We express this as H¹(X, ℝ)=ℤ², indicating the first homology group.

To further illustrate, consider a 3-dimensional sphere:

Within this sphere, any 2-dimensional shape can be contracted to a point. Unlike earlier examples confined to the surface of the sphere, here we can manipulate shapes inside the 3D structure. The k-cycles are classified within Hk(X, ℝ). Since all 1-cycles collapse to a point in a 3-sphere, we find H¹(X, ℝ)=0. Similarly, the 2-cycles also contract to a point, leading to the same conclusion.

In essence, the dimension of Hk(X, ℝ) informs us about the quantity of (n-k)-dimensional holes present in X, where n signifies the dimension of X. For instance, in the case of the torus, H¹(X, ℝ) is 2-dimensional due to the presence of two distinct holes.

To gain a deeper understanding, consider exploring a punctured 3-sphere, where a smaller sphere is removed from the center.

A key term in this discussion is "representative." As noted, there are infinitely many distinct k-cycles that can be deformed into one another. Each of these can be considered a representative of its respective equivalence class.

Geometry: An Overview

In this article, "geometry" will specifically refer to algebraic geometry, which involves the examination of shapes defined by the zero sets of polynomials. If you have background knowledge in linear algebra, you may recall that this field deals with zero sets of linear equations, resulting in straightforward shapes like planes and subspaces.

Linear algebra is largely resolved, yet introducing exponents to equations opens a vast and active field of study—this is algebraic geometry, where one transitions between the geometric interpretation of zero sets and the algebraic manipulation of these equations.

A smooth algebraic variety, or simply "variety," is a geometric space, X, described by the zero sets of polynomials (over the complex numbers) that possess a “smooth” structure, as one might learn in calculus. While this explanation omits numerous technical details, it is essential to note that we typically work within projective space, which will not affect the overarching ideas.

As we’ve seen, several varieties are already present in our discussion: the 2-dimensional sphere emerges from a quadratic equation, while the torus is defined as an elliptic curve derived from a cubic equation. The terminology can be unusual, as an elliptic curve refers specifically to a 2-dimensional torus.

When operating within the realm of complex numbers, real dimensions invariably appear as even. For example, a 1-dimensional curve translates to 2 real dimensions, while a 2-dimensional surface corresponds to 4 real dimensions. While this may seem intricate, it serves to underscore the nature of algebraic geometry.

Lastly, we introduce the concept of subvarieties. A subvariety of X is simply a subset that is also defined by zero sets of polynomial equations, thus qualifying as a variety.

The Hodge Conjecture: An Intriguing Question

The most straightforward interpretation of the Hodge Conjecture at this stage could be framed as follows: Given a cycle [A] in Hk(X, ℝ), is there a k-dimensional subvariety Y that can represent [A]? We refer to such a subvariety as an algebraic representative for [A].

Let’s take a moment to unpack this. Recall that A can take on complex forms and is fundamentally a topological concept that weaves around the holes in X. Can we reshape A into a “nice” form that is defined by polynomial equations?

If you assume the answer is clearly affirmative, you may be underestimating the stringent nature of being a subvariety. Conversely, if you believe the answer is a resounding no, you might be overlooking the extensive possibilities for deforming A without altering its class.

This basic version of the conjecture has been proven false based on our previous discussions. Remember, we are considering the complex numbers, so all subvarieties are even-dimensional, meaning there are no algebraic representatives in Hk(X, ℝ) under certain conditions.

However, even when we restrict ourselves to even dimensions, a further technical aspect complicates matters. The standard formulation of the Hodge Conjecture involves cohomology rather than homology, which introduces superscripts instead of subscripts. It’s noteworthy that these concepts are dual to each other. If X has a real dimension of n, we can interpret [A] in Hk(X, ℝ) as a class in Hn-k(X, ℝ).

This approach allows for an interpretation of cohomology via differential forms, facilitating numerical computations through integration. An elegant decomposition known as the Hodge decomposition exists under our assumptions about X, which utilizes harmonic functions. The decomposition organizes components by pairs of numbers that sum to the exponent.

For instance, we can express Hk(X, ℝ) as comprising parts labeled (0, k), (1, k-1), (2, k-2), up to (k, 0). The central segment consists of forms identified as Hodge classes, and this doubling occurs exclusively for even exponents.

A straightforward calculation, employing certain technical tools, demonstrates that any subvariety [Y] must reside within that central segment. In essence, every subvariety is a Hodge class. For example, if X is 6-dimensional in the complex sense and Y is a 2-dimensional subvariety, then [Y] occupies the (4, 4) section of Hk(X, ℝ).

If all of this feels overwhelming, you can simply view it as an additional “numerical condition” that must be satisfied. Since every subvariety is a Hodge class, we can ascertain that the basic version of the Hodge conjecture cannot hold true by identifying a non-zero class that is not a Hodge class.

The contemporary interpretation of the Hodge Conjecture posits that every Hodge class is algebraic. In other words, irrespective of how complex a Hodge class may be, it can be transformed into a genuine subvariety.

Progress Made Toward the Conjecture

Interestingly, the Hodge Conjecture has been confirmed in lower dimensions, thanks to Lefschetz's findings from 1924, which predate Hodge's conjecture formulation in 1950. Lefschetz demonstrated that for codimension 1, every Hodge class in H²(X, ℝ) is algebraic. By duality, this also confirms that every Hodge class in Hn-2(X, ℝ) is algebraic. Hence, the conjecture holds true for dimensions 1, 2, or 3.

Over the years, a few other instances have been validated, but only under stringent additional assumptions. Given the wording of certain sections in this article, it is apparent that I lean toward the view that the conjecture may ultimately be disproven, as I see no compelling rationale for believing we’ve sufficiently constrained the conjecture yet.

The historical narrative is lengthy and fascinating, and I will intentionally oversimplify it here for emphasis. Picture an individual proposing the naive conjecture, followed by someone pointing out that all subvarieties are indeed Hodge classes. This prompts curiosity about whether all Hodge classes are algebraic.

In 1961, Atiyah and Hirzebruch established that the integral version is false, leading to inquiries about the validity of the conjecture when moving from ℝ to ℚ. This is the current state of affairs.

Unlike the Riemann Hypothesis, which is backed by substantial evidence, the Hodge Conjecture feels like a work in progress, having stagnated following several refinements. To this day, we are uncertain of its truth when X is 4-dimensional and defined by a single polynomial equation!

It seems increasingly plausible that further necessary conditions will be discovered regarding algebraic classes, allowing for a refined conjecture that can be proven. It’s worth noting that if a counterexample arises that is evidently pathological (in a way that permits a clean reformulation of the conjecture to exclude the example), the $1 million prize will not be awarded.

This video, titled "What is the Hodge Conjecture?" provides an introductory look into the conjecture, its significance, and its implications in mathematics.

The second video, "The Hodge Conjecture (Part 1)," delves deeper into the complexities of the conjecture, exploring its mathematical foundations and challenges.