Chapter 1: Introduction to Lagrange Interpolation

In this piece, I celebrate my 100th article by delving into a topic close to my heart—one of my favorite mathematicians, or perhaps physicists: Joseph-Louis Lagrange.

It’s widely accepted that for any set of distinct points in a plane, you can construct a unique polynomial of degree ( n-1 ) that passes through all those points. For instance, two points define a straight line, while three points create a parabola. The traditional method for finding this polynomial can be quite tedious, involving the setup of a general polynomial of degree ( n-1 ):

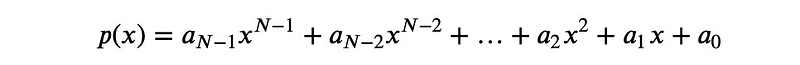
After this, you’d substitute your points into the polynomial, resulting in a system of equations that needs solving. This method can feel cumbersome. Fortunately, Lagrange's approach offers a much simpler solution. The key takeaway is that ( n ) points uniquely determine a polynomial of degree ( n-1 ). This uniqueness means that regardless of how you express the polynomial, it remains the same.

Let's take three distinct points as an example:

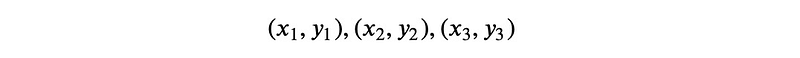
We know there exists a unique quadratic polynomial that intersects all three points. The challenge lies in expressing it correctly. Consider the following expression:

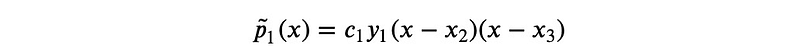
If we substitute ( x_1 ):

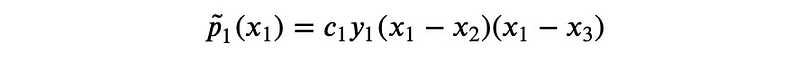
And similarly for ( x_2 ):

This method allows us to ensure the polynomial passes through a specific point. By selecting a particular constant:

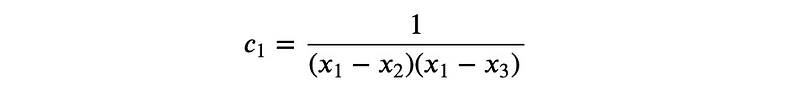
We can derive:

Thus, when ( x = x_1 ):

This allows us to selectively enable the desired points for the polynomial to intersect. By applying the same process for all points, we can sum them up:

Substituting ( x_1 ) results in the other terms being nullified by the numerators. This process continues for ( x_2 ) and the remaining points as well. The final result is a combination of three polynomials of degree 2, making it a polynomial of degree 2 overall. Given that the polynomial through the chosen points is unique, we have successfully identified the interpolating polynomial in a specialized form without needing to solve a system of equations.

Moreover, this method can be easily extended to ( n ) points. For a set of points:

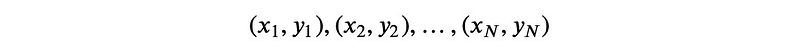
The unique interpolating polynomial can be articulated as:

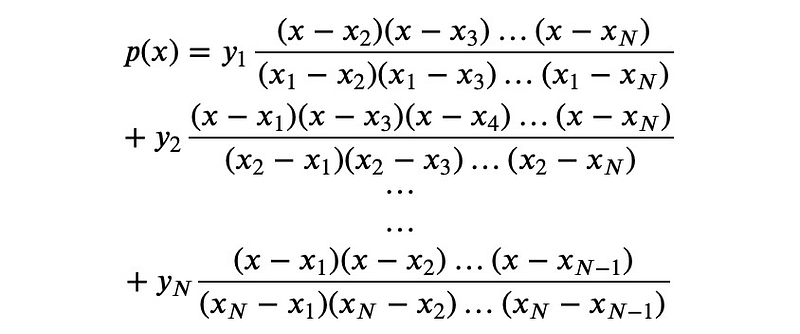
This is the classic Lagrange interpolation formula. When I first encountered it, I found it challenging to memorize. Typically, mathematical theorems are presented with proofs that can be less helpful for understanding. By attempting to rediscover the formula myself, I found a method that made it easier for me to remember, allowing me to reconstruct the formula within minutes.

Chapter 2: Conclusion

In conclusion, Lagrange's interpolation method provides a more intuitive and simplified approach to constructing polynomials that fit through given points, making it a valuable tool in both mathematics and applied fields.