Exploring the Basics of Rational Numbers and Their Properties
Written on
Chapter 1: Understanding Rational Numbers
The essence of rational numbers is often overlooked in traditional education. Reflecting on my own schooling, I realize that the core principles of rational numbers are not easily imparted; they are discovered through personal mathematical exploration. This essay aims to elucidate the foundational aspects of rational numbers using basic arithmetic logic and geometric insight, concepts that are accessible to all.
Before diving into rational numbers, let’s first examine the fundamentals of numbers.
Section 1.1: The Fundamentals of Numbers
The concept of numbers and arithmetic emerges from our innate need to count. Counting is so fundamental that it transcends humanity; many animals exhibit basic counting abilities. Humans, however, elevate this skill to new heights.
Richard Dedekind was one of those thinkers who reached profound levels of understanding in this area. He famously defined counting as the process of creating an infinite series of positive integers, where each number is defined by its predecessor.
To clarify Dedekind's definition: counting begins at an arbitrary starting point (like zero) and continues by adding one for each unique occurrence of an element.
Section 1.2: Beyond Simple Counting
While counting is a powerful tool, it is only the beginning of human arithmetic. The four fundamental operations—addition, multiplication, subtraction, and division—allow us to manipulate numbers in more complex ways.
Addition combines quantities, while multiplication can be seen as repeated addition. Conversely, subtraction determines the difference between two quantities, and division tells us how many times one number can be taken from another. Unlike addition and multiplication, which are always applicable, subtraction and division have constraints that lead us to concepts such as negative and fractional numbers.
This brings us to the concept of Rational Numbers, denoted as 'Q', which encompasses counting numbers, negative numbers, and fractions.
Chapter 2: Properties of Rational Numbers
In this video, "Learn Rational Numbers In 7 min," you can discover the essential properties of rational numbers quickly and effectively.
The rational number system has two vital characteristics: completeness and self-containedness. For instance, any two rational numbers can undergo the four fundamental operations, producing another rational number. However, division by zero remains an exception, a concept that merits deeper exploration.
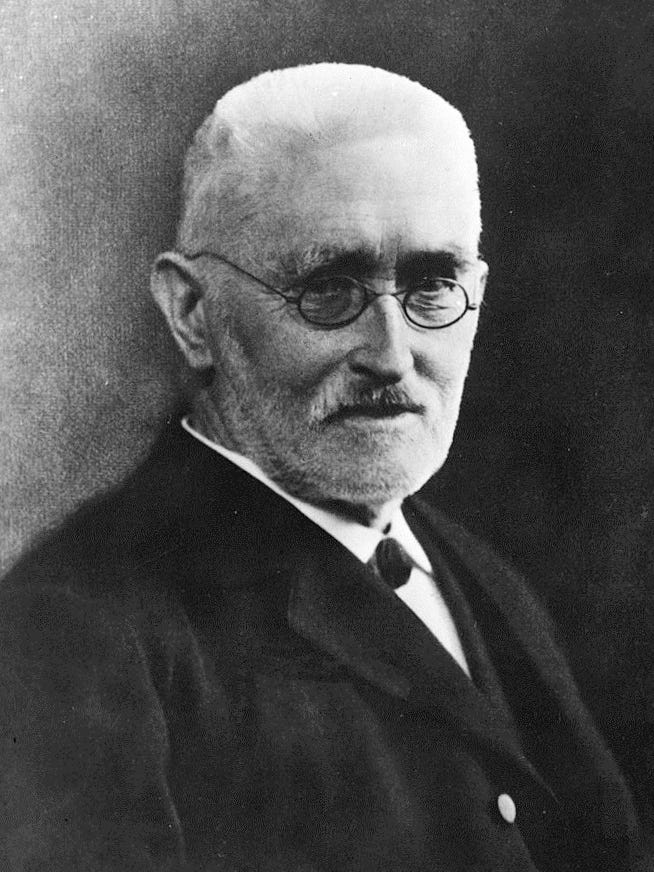
When we visualize rational numbers arranged from smallest to largest, we see a well-structured number line that extends infinitely in both directions.
Section 2.1: Extended Properties of Rational Numbers
One critical property of rational numbers is transitivity: if ( a > b ) and ( b > c ), then it must follow that ( a > c ).
This may seem intuitive, yet it is essential to recognize that not all mathematical areas follow such straightforward logic. Using geometric intuition, we can illustrate that if ( a ) and ( c ) are distinct, ( b ) will occupy a position between them on the number line.
Another intriguing property is that between any two distinct rational numbers, an infinite number of additional rational numbers exist. Visualize two points on a ruler; if you continually divide the interval between them by two, you'll never cease to find new numbers, leading us to the fascinating realm of infinitesimals.
The video "Master the Fundamentals of Rational Numbers Grade 7 and 8" delves into the essential concepts and properties of rational numbers for students.
Section 2.2: Rational Numbers and the Dedekind Cut
Consider a rational number ( a ). All other rational numbers can be classified into two categories: A1, containing numbers less than ( a ), and A2, which includes numbers greater than ( a ). The question arises: to which group does ( a ) belong?
This is not a straightforward answer. According to Dedekind, one can classify ( a ) in either group, leading to fascinating implications for understanding the continuity of the number line.
In closing, Dedekind's exploration ultimately led to the creation of the Dedekind cut, a pivotal concept in defining real numbers.
Reflecting on these concepts, I find myself grateful that I did not learn about rational numbers in a conventional classroom setting. Perhaps I wasn't ready for such complexity at that time—or even now!