The Mathematical Derivation of the Catenary Curve
Written on
Chapter 1: Understanding the Catenary
A perfectly flexible chain that is held in equilibrium and subjected to gravitational forces takes the form of a curve known as a catenary. This term was first introduced in 1690 by the renowned Dutch polymath Christiaan Huygens in correspondence with the distinguished German scholar Gottfried Leibniz.
The catenary bears resemblance to a parabola, which led the Italian scientist Galileo Galilei—who was the first to examine it—to mistakenly categorize it as such. However, the accurate shape was determined independently by Leibniz, Huygens, and Swiss mathematician Johann Bernoulli in 1691. Their investigations were a response to a challenge posed by Jacob Bernoulli, Johann's elder brother, to derive the equation of the "chain-curve."

Figure 1: From left to right, Jacob Bernoulli, Gottfried Leibniz, Christiaan Huygens, and Johann Bernoulli.
The figures submitted by Leibniz and Huygens to Jacob Bernoulli can be seen below, which were later published in the Acta Eruditorum, the first scientific journal in the German-speaking regions of Europe.
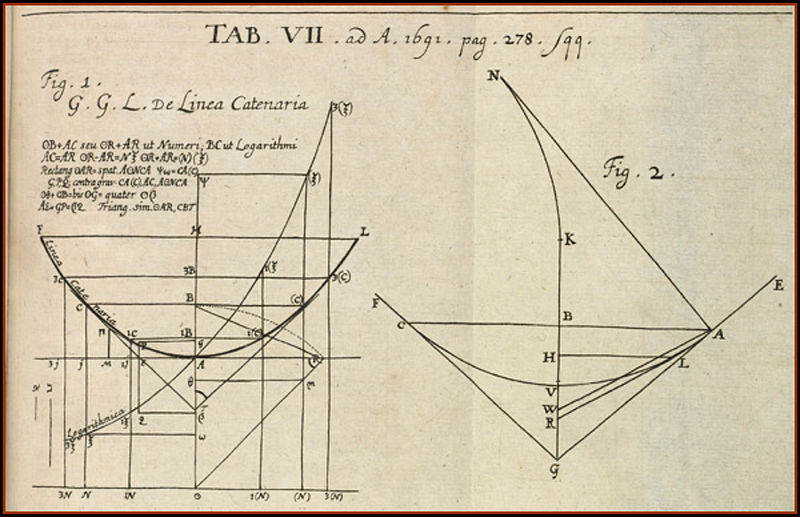
Figure 2: The illustrations provided by Leibniz (left) and Huygens (right) for Jacob Bernoulli’s publication.
Johann Bernoulli was pleased to have solved a problem that had eluded his brother Jacob. In a letter written 27 years later, he expressed his triumph:
"My brother's attempts were unsuccessful. Fortunately, I had the fortune to solve it completely, though it cost me a restless night of study. The next morning, brimming with joy, I rushed to my brother, who was struggling with this intricate problem, still believing it was a parabola. I told him to stop torturing himself, for the catenary was completely different."
— Johann Bernoulli
Finding the Equation of the Catenary
To derive the catenary's equation, we make several key assumptions:
- The chain (or cable) is suspended between two points and hangs under its own weight.
- The chain (or cable) is flexible and possesses a uniform linear weight density (denoted as w).
This analysis closely follows Simmons' work. For simplicity, we will let the y-axis pass through the lowest point of the curve. The distance from the minimum to the point (x, y) is represented by s. The forces acting on this segment include the tensions T₁ and T₂, and its weight w·s (refer to the figure below). The first two forces are tangential to the chain.

Figure 3: The parameters and variables utilized in the analysis.
For the segment to maintain equilibrium both horizontally and vertically, the following conditions must be satisfied:
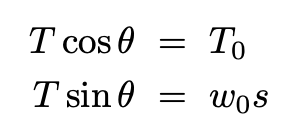
Equation 1: Equilibrium conditions for the segment of length s.
We need to solve the following differential equation:

Equation 2: Differential equation we need to solve.
Next, we will express this equation solely in terms of y and x. By differentiating, we obtain:
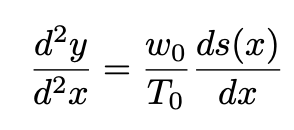
Equation 3: The derivative of Equation 2.
The derivative ds/dx can be represented in terms of dy/dx as follows:
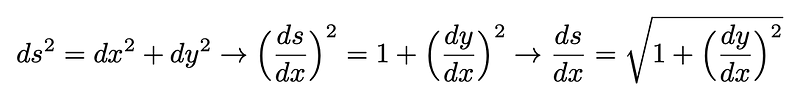
Equation 4: The derivative ds/dx expressed in relation to dy/dx.

Figure 4: The infinitesimal triangle used in Equation 4.
Substituting into Eq. 3, we have:
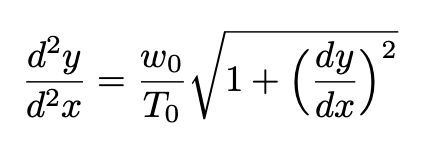
Equation 5: The differential equation of the catenary.
To simplify the solution of Equation 5, we introduce the variable:
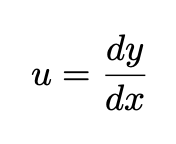
Equation 6: Definition of u used to solve Equation 5.
Using Equation 6, we can rewrite Equation 5 as follows:
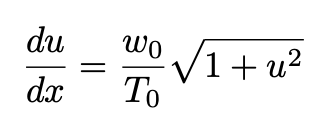
Equation 7: Equation 5 reformulated in terms of the variable u.
This equation can be integrated using variable separation alongside a straightforward trigonometric substitution u = tan(θ):
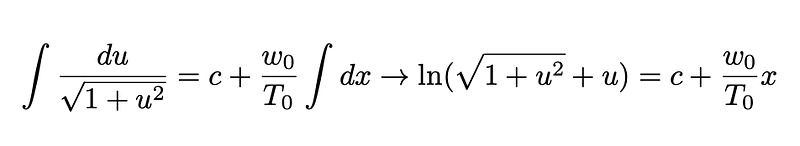
Equation 8: Equation 7 following integration.
Since the y-axis passes through the curve's minimum, we have:
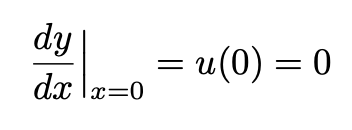
Equation 9: The variable u equals zero at the curve's minimum.
Plugging Equation 9 into Equation 8 gives us:
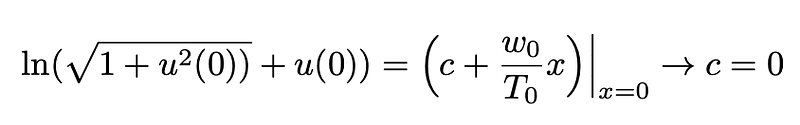
Equation 10: Using Equation 9 to find c in Equation 8.
Substituting c=0 into Equation 8 and solving for u yields:
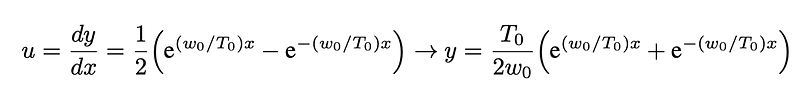
Equation 11: The solution of Equation 5, which results in the equation of the catenary.

Figure 5: Three instances of catenaries: A chain suspended from two points, overhead power lines, and the silk of a spider's web forming multiple catenaries.
Exploring the Catenary: Video Resources
To deepen your understanding of the catenary curve, check out the following videos:
The first video titled "How Do You Find The Shape of Hanging Rope? Classic Physics Problem - YouTube" explains the fundamentals of the catenary curve in relation to hanging ropes.
The second video titled "The Catenary (hanging chain), how it was first solved - YouTube" discusses the historical context and the mathematical solutions to the catenary.
Thank you for reading! Your feedback is always appreciated. For more insights into math, physics, machine learning, and other topics, feel free to visit my LinkedIn, personal website at www.marcotavora.me, and GitHub!